内含波动率下期权市场价格如何计算

来源：【赢家江恩】责任编辑：liuyanshuang添加时间：2015-03-13 09:57:35

　　内含波动率法假设个股期权的市场价格反映了股票的现时波动率，那么我们可以用布莱克一斯科尔斯公式计算标准差。内含波动率就是使理论价与市场价格相等的标准差，我们用δ表示。

　　由于从该模型不能直接简单地解出标准差，我们要用试错法依次对δ取值，代入公式计算，直至使公式得出的理论价格与期权市场价格相等的δ值产生，这就是所求。图4.10表示的是内含波动率的求解顺序。

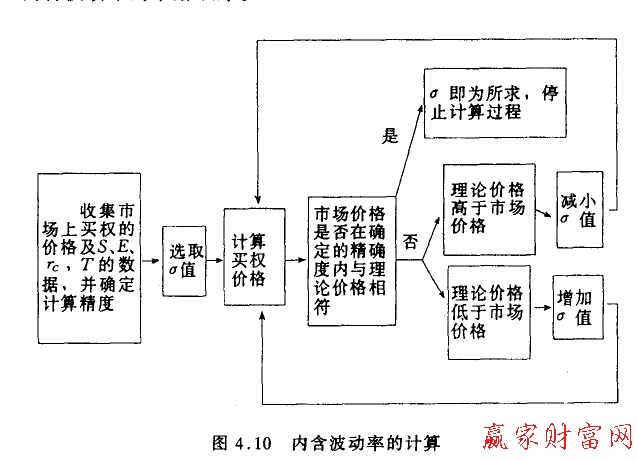
　　由于δ是股价的波动率，标的股票相同、到期时间相同的期权计算出的波动率应是相同的，但由于种种原由。包括定价模型自身的局限性，从相同标的资产的同期期权计算出的内含波动率是不同的。为进行调整，有的对不同的内含波动率求简单算术平均.还有的取加权平均，还有的只取执行价格与市场股价相近的期权的内含标准差。

　　当执行价格与股价相等时，买权价格与股价波动率几乎是线性关系。Brenne:和Subrahmanyam在1988年经过实证研究表明.买权处于平价时.有以下关系成立:

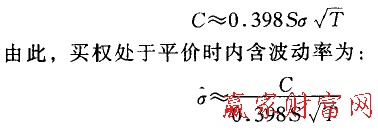
　　其中C为买权的价格。

　　在使用内含波动率的过程中存在一个矛盾，为计算内含波动率，就必须假定期权的价格是正确的，于是由此计算出的内含波动率就被用于对别的期权进行定价，得出的理论价格将与现实价格进行对比以确定市场价格是否合理，是否存在高估、低估的情况。这样就有必要假定某时刻期权定价是正确的，另一时刻其定价又是偏误的，至于何时的定价是错的，我们不能确定。

　　正是波动率价值的不确定性，使期权成为最有吸引力的金融工具之一。如果市场投资者对波动率的预期相同，期权的定价就是正确的，那也就没有必要进行买卖交易。只要当投资者对波动率的评价具有差异，就认为期权的价格不是合理水平，由此导致了期权的买卖。

如果想了解江恩理论和财务分析知识，欢迎访问赢家江恩。